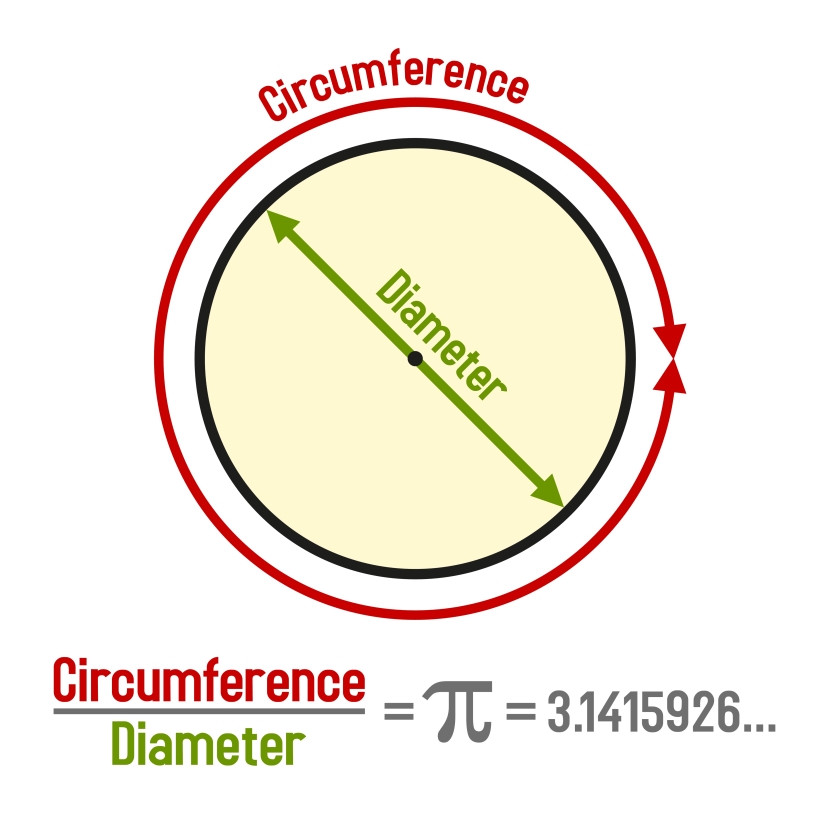
We define Pi as the ratio of a circle's circumference to its diameter.
In other words: all the way around a circle divided by all the way across it.
The picture illustrates this perfectly.
One could ask how easy or difficult it is to measure the number Pi.
We have visited Fyrkat which is an old Viking Casstle in Hobro, Denmark.
Fyrkat has a beautiful shape - it's formed as a perfect circle and it's from the Vikings Age.
In fact it's dated back from around year 970.
The Viking city of Fyrkat

We used the app Endomondo on our smartphones to measure the lengths. The circumference was 401 meters and the diameter was 120 meters. The ratio is 3.34.
The very same day we measured the circumference of a perfect plate and divided it to the diameter. Our result was close to 3.18.
This highly indicate that it's not trivial to get digits of Pi from pure measuments. Feel free to read more about the nature of Pi in the Articles under the fane Information.
Pictures of our measuments



The clear pictures shows us the Viking City Fyrkat from above.
There are 3 other known Viking Castles in Denmark, namely Aggersborg, Nonnebakken and Trelleborg. They served primarily as a defense facility.
The very last picture shows us the measument of a single plate.
How many digits of Pi do we really need?

Pi is very beautiful, unique and aesthetic in itself and so are the digits. Clearly for a memory purpose we really have no limit for digits of pi. The Pi Matrix Challenge have the limit of 10,000 digits. But how many digits do we need to describe our world and universe? If we want to describe our world and universe we need not many digits of Pi. Marc Rayman, the chief engineer for NASA's Dawn mission, claimed that we need more than 15 digits of Pi for the calculations in space. In his context he is actually right. The British mathematician Marcus du Sautoy explains the number Pi in a nutshell in his amazing show and explains why we need no more than at least one hundred digits of Pi. In fact he claims that we only need the first 39 digits of Pi to calculate the circumference of a circle, the size of the entire observable universe, accurate to the radius of a single hydrogen atom.