Is Pi a normal number?
Pi is believed to be a 'normal' number. This means that no digit (or sequence of digits) occurs more frequently than any other. So any number you can possible imagine will appear in Pi somewhere. It is not true that an infinite, non-repeating decimal must contain ‘every possible number combination’. The decimal 0.011000111100000111111… is an easy counterexample.
However, it's been proved that almost all irrational numbers are normal. But very few specific examples are known. It turns out to be extremely difficult to find a proof for specific cases. The first example for a known normal number in base 10 was introduced by David G. Champernowne in 1933.
Today it has still not been proved whether Pi is a normal number or not.
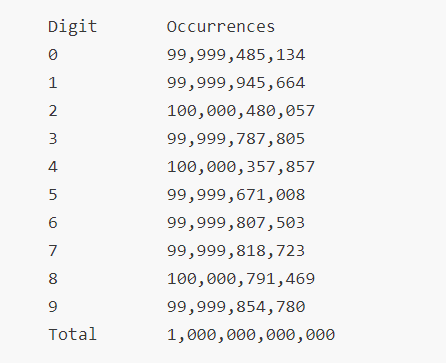
In 2003, Yasumasa Kanada published the distribution of the number of times different digits appear in the first trillion digits of pi as shown. His results imply that these digits seem to be fairly evenly distributed, but it is clearly not enough to prove that all of Pi would be normal.
Find your birthday in Pi
Click the button to enter your birthday.
